A concept used in one-way hash function cryptography attacks, BIND attacks, in roulette, lottery, even estimating DNA sequence collisions or the chances of duplication of your SSN no.(if you are American that is); the birthday paradox is a phenomenon that deals with the probability of repetition.

Traditionally it started with trying to figure out what the chances are of two people having the same birthday (of course excluding twins). Assuming it’s not a leap year and that there is even possibility for each day to be a day of birth; the chances that G-one and Ra-one have the same birthday is 1/365; these two are independent events after all. Now if you ask what’s the probability that 2 out of 3 people under consideration share the same birthday; you are dealing with three combination of matches…3-1,1-2,2-3.
Let’s try to model these cases for k people… it gets a bit messy doesn’t it? Let’s look at it the opposite way, what are the chances of no repetition among k people? We can go about it in a linear fashion; proceed to find a workable pattern…
case1–deal with 1 guy… no repetition
case2 –2 guys; A has birthday on one of the 365 days, other guy B can have his on any day barring A’s to avoid collision; correct? So to have no collision B’s chances….364/365
case3—3 guys; C has chances 363/365 to avoid collision with A or B (A,B take up 2 different days out of the picture for C to have been born on)
and so it goes……the pattern being ,
for k people, no repetition chances for kth guy:
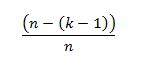
Where n=365
Now to calculate the likelihood of all these events, all these non-collisions, occurring in a sequence, we have
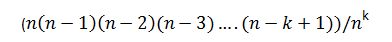
..a multiplication of the probabilities of independent events(independent because there is no real dependency of your birthday on another’s, unless you are siblings or there are multiple overlapping matches)
This can be presented as:
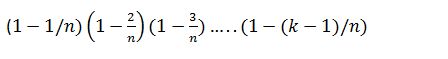
From Taylor’s polynomials:
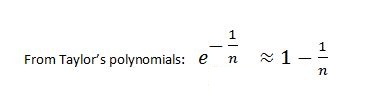
So our equation becomes:
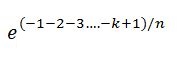
Now the sum in the exponent power numerator can be simplified as -k(k+1)/2; therefore the probability looks like this:
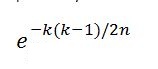
With this component we can compute a 100% chance of collision when k=n=365.What is the no. of people(k) required to have at least a 50% chance of repetition?
We solve like this:
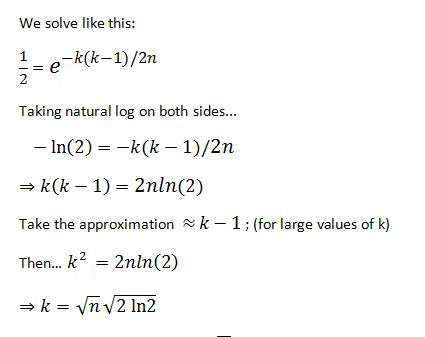
This gives us… k≈1.174√n ; which means that given ‘n’ no. of possibilities of occurrence of an event, we need 1.174 times the sqrt of n to have a 50-50 chance of the event repeating. This is significant; chances of collision are intrinsic to a lot of concepts.
For the birthday case which started all this; we see that with n=365, required minimum k becomes 22.49 or approximately 23 people (with a little bit better than half chance of a match).
Just another weird way to point out that you are not the only one to celebrate your b’day on a given day(ignore the rhyme), and that any gathering of 23 or more(in a classroom, your office,on the bus) will have a pretty realistic chance of producing a pair or more who share a common b’day.(now don’t go looking for people who match your b’day; you might be disappointed, this concept doesn’t set a particular day as constraint, it can be any day that pops up to have a collision)
We will look at some of its applications in the next segment..








1 Comment