Explanation of (a+b)^2 = a^2+2ab+b^2
Mathematics is fun. This simple formula is taught to us since the first days of algebra classes and is used till the end of time. But the formula has never given us the real life perception. Recently I came across this explanation of (a+b)^2 and found it extremely interesting. Let’s have a look:
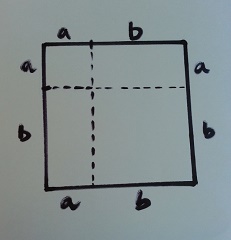
1. First we take a line segment and arbitrarily divide it into two segments a and b. Remember the section has been done arbitrarily so that the formula can be proved for any values of a and b.
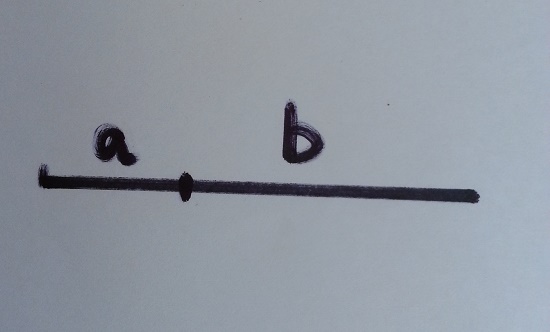
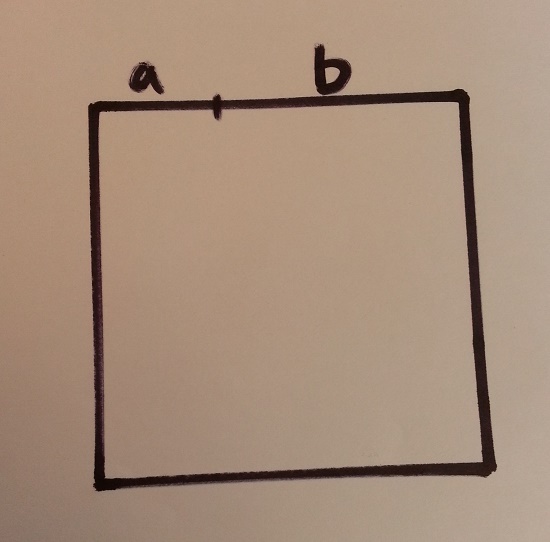
2. Now we know that the length of the line segment is a+b. If we construct a square having side (a+b), then area of the square will be (a+b)^2.
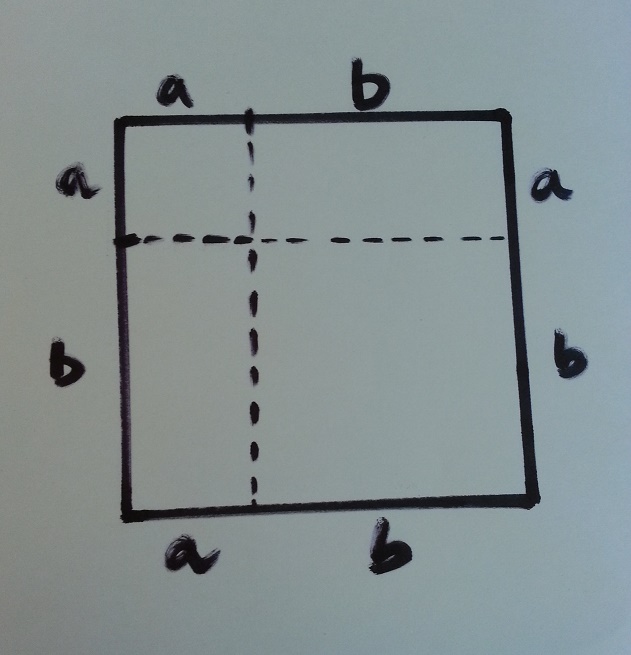
3. Next, we divide the square as shown in the figure. So we get 2 squares and two rectangles.
4. The squares and rectangles are designated by the alphabets.
Area of square P= a^2 square units
Area of square S= b^2 square units
Area of rectangle Q= ab square units
Area of rectangle R= ab square units
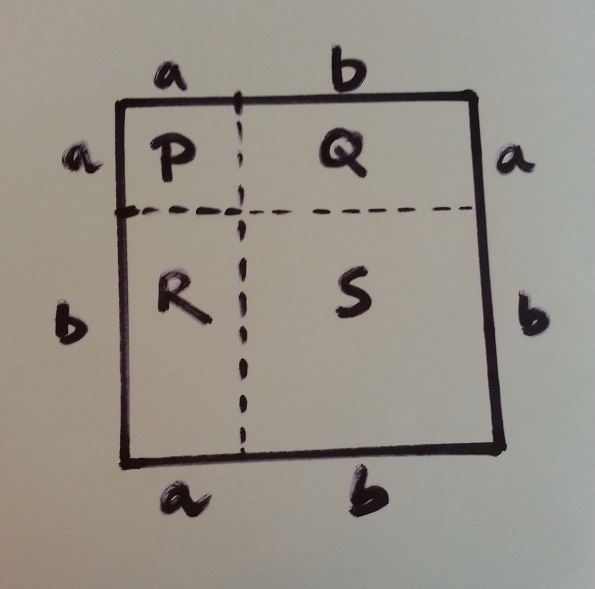
5. So adding u both sides, Area of (P+Q+R+S)= a^2 + ab + ab + b^2
that means (a+b)^2= a^2 + 2ab + b^2
Isn’t it fun?







Leave a Reply